【Postmortem】HACK TO THE FUTURE for Youth+

画像は公式Visualizerよりお借りしています
はじめに
投稿はおよそ半年ぶりになります。コンテストに参加すること自体、かなり久しぶりでした。この記事は10/10にAtCoderで行われました、FIF様主催の「HACK TO THE FUTURE for Youth+」の記事になります。コンテストの詳細はこちら
今回のコンテストはチームmonk1としてstatiolakeさんとともに参加しました。長期間のブランクで実装速度が遅くなっていたところstatiolakeさんに助けられまして、最終順位は本戦ページのチーム順位表で30位でした。個人的にはかなりうまくできたと感じているので、自身の備忘録も兼ねて書きます。
解法選び
今回のコンテストでは、短いコンテスト時間内でどれだけの記録を出せるかに拘って取り組んでみました。コンテストとはそもそもそういうものなのでは?と思われたかもしれませんが、今回のコンテストではコンテスト時間が4時間しかなく、元々コーディング速度が致命的に遅い私ではたとえ筋が悪くても実装が簡単な方が好順位を取りやすいことが多いため解法があまり適切でなかったりします。自分の成長のためには適切な解法で取り組みたいところですが、今回はコンテスト時間内の記録に挑戦しました。
今回の問題を見た印象ですが、一言でいうと「プログラム完成できなそう」という感じでした。私は考察のため最初の30分ほどはA問題を手動で試しつつ考えていましたが、思いついたのはどれも4時間のプログラムには落とし込めないような解法ばかりでした。(上位の方が普通に提出できている解法は私にはとても時間がかかるものばかりで間に合わないのです)
そこで、解法を選ぶ前にチームとして前提となる方針を固めました。以下の通りです。
・問題Bと問題Cのプログラムはほとんど同じものを使用することにし、二人で一つのプログラムを書く
・試せる解法は1~2つくらい
上の方針がなければ実装が絶望的でした。問題が難しく、それなりな解を出すのがひとまずの目標でした。
そのうえで、各解法についてどのくらいかかるかを考えました。
・ブロックの置き方でビームサーチ(4時間ではベースが完成しない。)
・ブロックで各印を覆いきってから最小全域木にする(4時間では覆うところまでかな・・・。効率の良い覆い方も見つからず、最小全域木にもならないかも)
問題が難しくこのままではどの解法でも完成させられない・・・。statiolakeさんには入力を受け取った順に印を1*1のミノでつなげるプログラム(さすがにこれを提出するつもりはなかった)を書いていただきながら悩むこと約1時間、まあまあな解法で実装がかなり簡単なものを思いつき、それを実装することにしました。(その解法は「最終提出プログラムの戦術」参照)
最終提出プログラムの戦術
最終提出プログラムの戦術とは銘打っていますが、最終提出とつけるほど提出はありません。ソースコードの変遷はかなり一本道でした。「解法選び」の部分で書きましたが、4時間のうちに書くことのできる、非常にお手軽な解法となっています。
戦術はかなり明確にパート分けされています。具体的には
1. 1*1で各点をできるだけ低コストになるようにつなぐ(最善ではなくそれなりくらいのコストで。A問題26万点程度で、出力例にあった1*1を使ったつなげ方では30万点程度だったことを考えるとそれなりの無駄があります)
2. 1*1以外のポリオミノをランダムに埋め込んで重なった1*1のポリオミノを取り除くことでコストの削減を狙う
という戦術です。1については私は4時間では実装できないのですがここはチーム戦ということでチームメイトを頼り、私はその1*1の置き方が与えられた仮定の下で2の関数を作成していました。
ということで1の説明は私はできる自信がないので割愛いたしまして、2の説明をします。ポリオミノを埋め込んで1*1を取り除くというものについて下に図を載せておきます。
(1*1の接続例)

(置いてみるパターン1)

上のパターン1ではコスト3を一つ置くことによりコスト1を4つ取り除いています。
(置いてみるパターン2)
上のパターン1ではコスト2を一つ置くことによりコスト1を8つ取り除いています。
プログラムは10000パターンランダムにおいてみて最も節約できたものを置きます。そしてかぶる1*1ポリオミノを取り除きます。取り除き方から、無駄は多いですが必ず全印がつながっていることがわかります。一個置き換えただけでは大差ないので、置き換えた後の盤面にまた先ほどの操作をしてみます。1*1以外のポリオミノと重ならない置き方のみ試します。たいていは50個も置き換えればもう節約できなくなります。
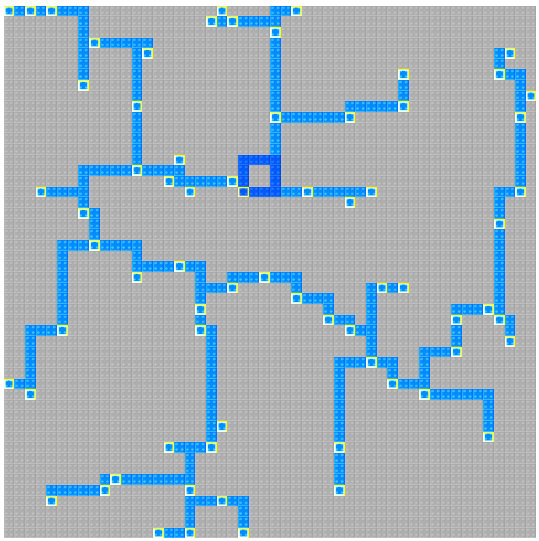
そうすると意外にもきれいに置いてくれています。
(2を行う前)
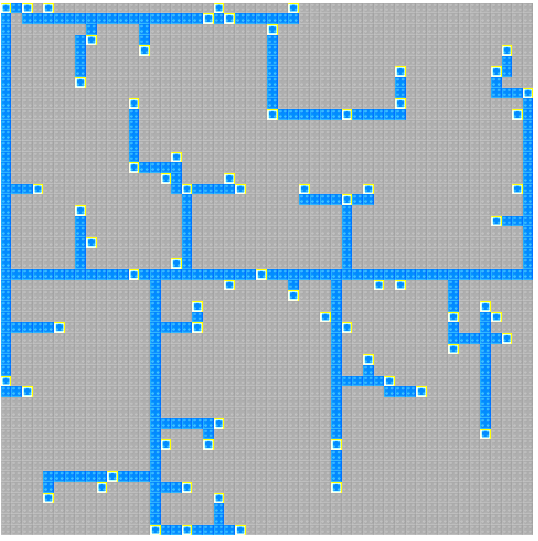
(2を行った後)
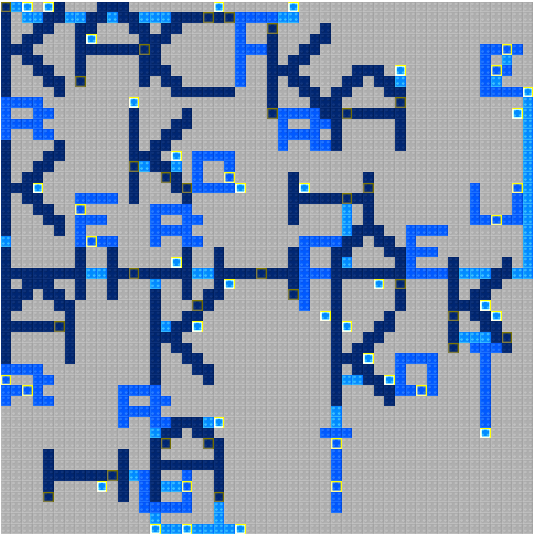
(ん?一番右の列と一番下の行が全く置き換わっていない・・・?バグでした。コンテスト中に気づきたかった。)
あとは局所解な可能性があるので盤面を1で得たものにもどしてやりなおすということを時間の限り行うのみで、最終的に一番よくできた結果を出力します。
2の部分の実装はかなり簡単な方で、私でも間に合わせることができました。(もし気になった方がいればmontplusaまたはstatiolakeさんの最終提出からoptimize()という関数を参照してね)
時間に余裕があれば、最後に不要な1*1ミノも取り除ければもう少しスコアが上がります(コンテストには間に合いませんでしたが、statiolakeさんが実装してくれました)
おわりに
今回のコンテストのような短期間のコンテストには苦手意識を持っていたのですが、非常に楽しく取り組めました。特に、今回は50*50のマスと比較的エリアが小さく人間でも楽しめるパズルゲームだったこともあり、プログラムの結果と人間の結果が比較できたりととても面白かったです。
今回チームを組んでくれた方、ともに4時間競った他チームの方々、今回のコンテストを運営してくれた方々、本当にありがとうございました。