はじめに
今回のコンテストでは6位と自分の中ではかなり良い順位ではあるんですが、一方で最上位に数歩届かず悔しい思いもあります(もともとLeaderBoardで雲の上とみていた憧れの人たちとLegendリーグでマッチングしているだけでもうれしいんですが)。そこで、次回こそは勝ってやるんだという気持ちでもう少しまとめてみます。
AIの方針はPostMortemにすでに書いた通りなのですが、もう少しだけ具体的にどう実装していたかを書き残しておきます。また最後の「解法の選択」はより次回以降のコンテストのために今の自分をまとめておこうと思い書きました。(次のコンテストまで意外と期間が空いたりして今の自分が得た知見が失われていたら嫌なので・・・)
結構長くなりますので、読んでいただける方は目次から気になるところだけ読んでいただけたら。
前提となっている自分のPostMortemはこちら
いくつかのトピック
ユニットの割り当て
以下で説明するのはあくまで自分のbotの元となるアイデアです。
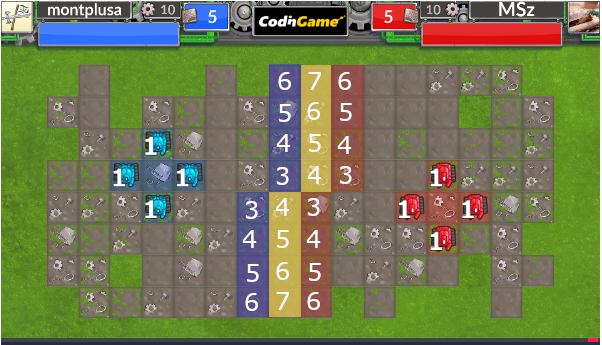
下のような場面を考えます。
(これはPostMortemの衝突地点の話で使っていたものです。)

DefencePoint(青)は自分のユニットのほうが近いマスなのでまずはDefencePointを確実に塗りたいところ。
まずは自然にこれらの衝突地点に一番近いユニットを割り当てるというのを考えました。どの衝突地点から割り当てるかで変わってきますが、以下が一例です。
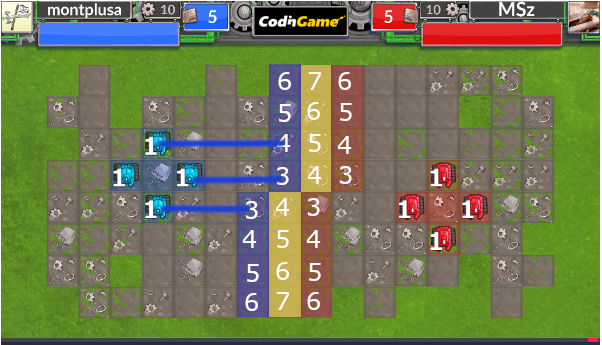
このように3体を配置したところで、まだ割り当てていないユニットではDefencePointを守り切れない(残っている一体は相手よりに先に到達できないので向かっても確実に塗れるとは限らない)ので手詰まりになってしまいました。
ここで、DefencePointは本来「順当にいけば確実に塗れるはずの場所」だったことを思い出すと、DefencePointを担当したユニットは絶対に敵ユニットと相殺されない、つまりその他のDefencePointも担当できるのでは?という考えが浮かんできます。
具体的には以下のようにDefencePointから距離が増加する方向へは複数のDefencePointを担当することができます。これは各衝突地点を頂点とした有向グラフとして保存しておくと何度も割り当てを考える際に比較的高速に処理が可能です。

(このほか衝突地点はおおよそのケースで64に収まるのでbitboardをつかって高速にする方法があります。が、今回は全力で高速化、というほどまでは詰めなくても割り当て速度が問題になることはなかったです)
一例として、この複数を担当することを考えると、このような割り当てを考えることができました。すべてのDefencePointを塗ることができ、また、いくつかのNeutralPointにも割り当てることができるようです。
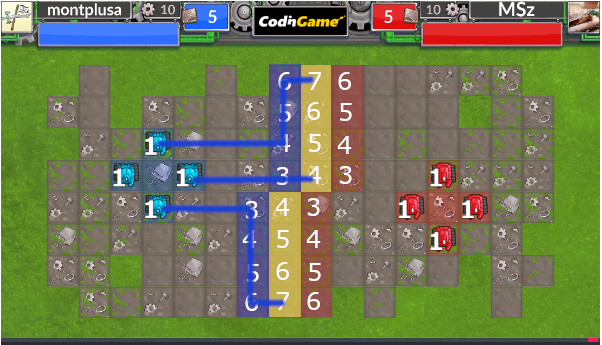
加えて、相手より2ターン早く到達できるDefencePointには最前線へのスポーンも有効です。これも考慮することにより、以下のような割り当ても可能になります。
(黄色の線は新たにスポーンさせ、そのユニットに割り当てていることを明確にするために色を変えただけです)
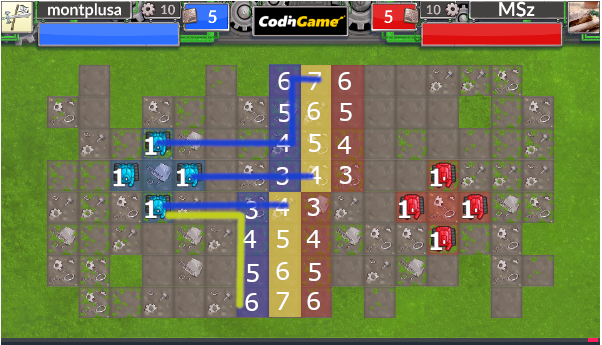
これによりさらに割り当ての幅が広がります。あんまり変わらないように見えるかもしれませんが、中央に一人多く送り込むことができたりするだけでかなり多くの有利が取れる場合があります。
最前線に間に合わないユニットの割り当ても同じロジックで考えることができます。例えば、上での到達ターン制限を+1すると1ターン遅れて到着するものも考慮することができます。特にNeutralPoint(到達に必要なターンが両者同じマス)では、最速で到達できるユニットが相手と同数の場合に、最速で到達できるユニット同士が相殺され、その次のターンに送り込んだユニット数勝負になることもしばしばあるので有効です。なお、2ターン以上遅れるとなると防衛の割り当て数などが不正確になっていくので、私はどの衝突地点にも2ターン以上で遅れてしまっているユニットは最寄りの衝突地点に向かわせていました。
大事だと思う衝突地点から順に割り当ててそれを行動として出力してもよいですが、これらの割り当てを得点化し、良いものを採用するとよりよい動きをしてくれるようになりました。
この例の試合では結果として序盤の中央勝負で有利をとることができました。
(うっすらと見える青、黄、赤はゲーム開始時点での衝突地点)
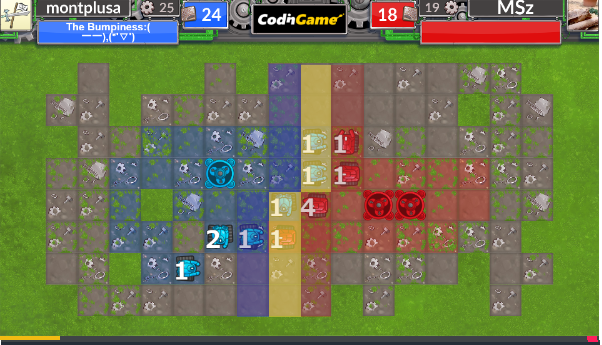
以下のリプレイでも真ん中一列をとることができ、これが勝因になりました。
https://www.codingame.com/replay/689120836
各地点間の距離計算
本当ならばマップ上のすべての地点間の距離を知りたいところですが、最大のマップサイズでは12*24=288頂点となってしまいとても50msでは考えられそうにないです。
そこで、各ターン必要になりそうな距離だけをいわゆるBFSによりに求めます。今回はRecyclerでいずれ緑化するマスがあるのが特に逆順で距離を求める際に悩みました。
1. 自分のユニットのいるマスを距離0、ユニットのいない自分のマスを距離1として、そこからBFS→自陣から各地点への距離がわかる
2. 相手のユニットのいるマスを距離0、ユニットのいない相手のマスを距離1として、そこからBFS→敵陣から各地点への距離がわかる
ここで、1.と2.で得た距離の差が2以下の点を衝突地点として登録します。
3. 衝突地点を距離0としてそこからBFSを衝突地点ごとに行う→各地点から各衝突地点への距離がわかる(注意:衝突地点への距離を衝突地点から逆にたどって求めているのでrecyclerによる緑化判定が少し複雑になります!)
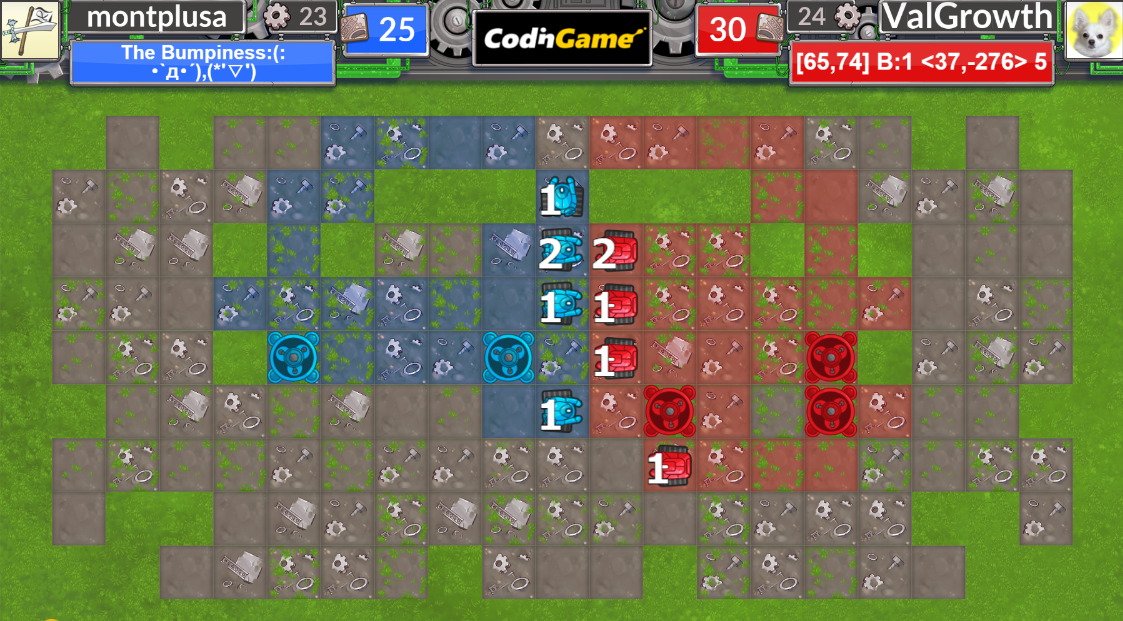
この場面での距離を見てみます。
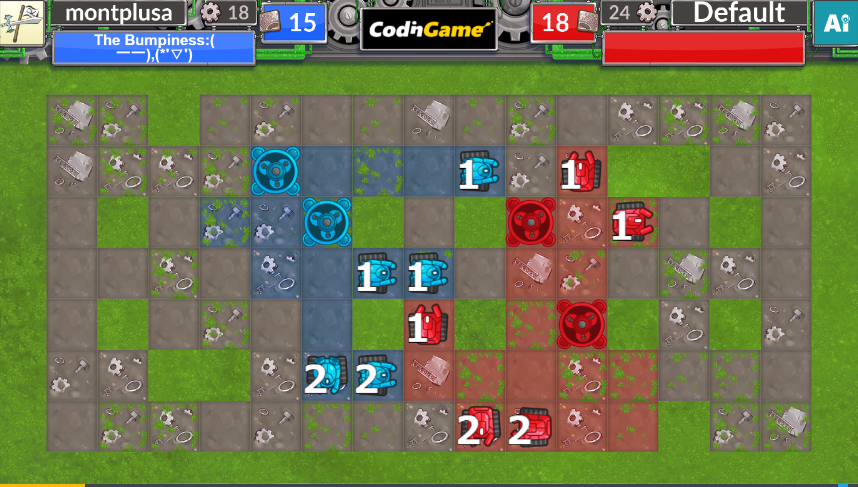
1.はこんな感じに。recyclerの影響で行けない場所があったり、遠回りを要求されているところがあったりします。
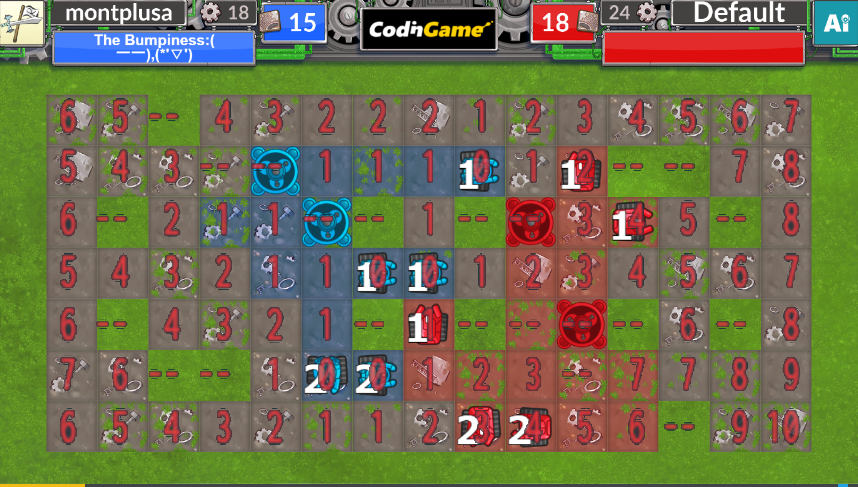
2.はこんな感じに。
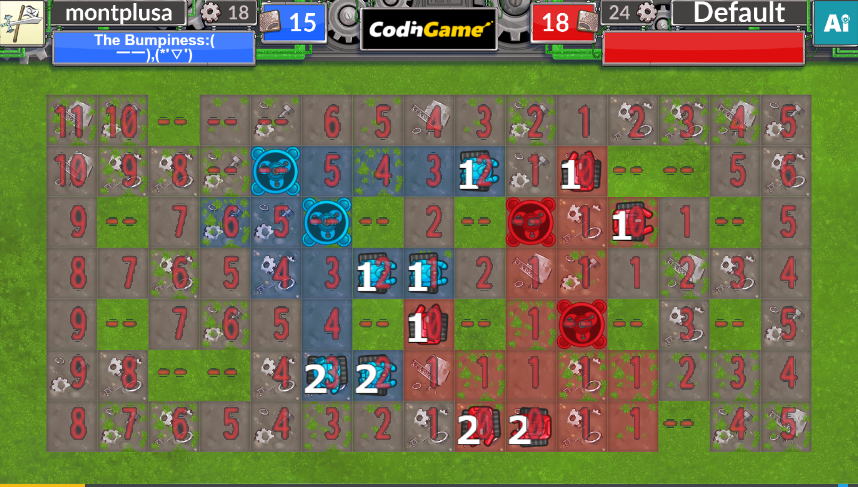
3.はこんな感じに。(下画像黄色の四角で囲んだ衝突地点についてBFSを行っています)
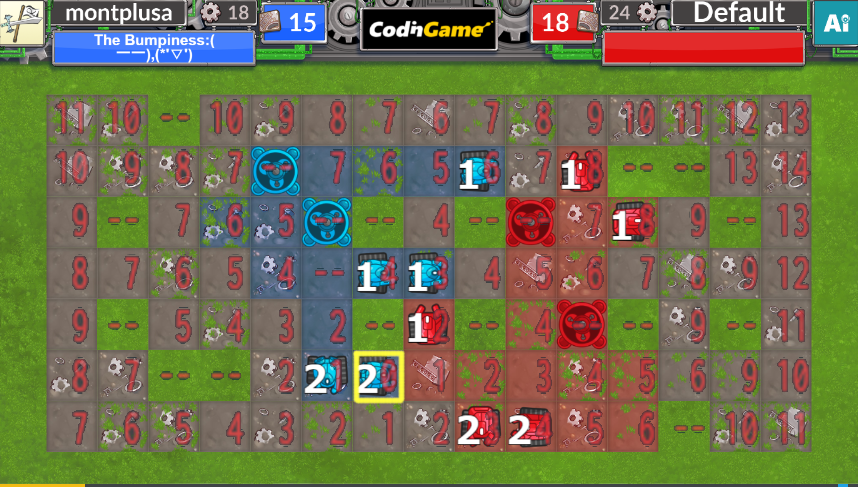
この3.は以下のような緑化による最短経路の違いに対応する必要があります。
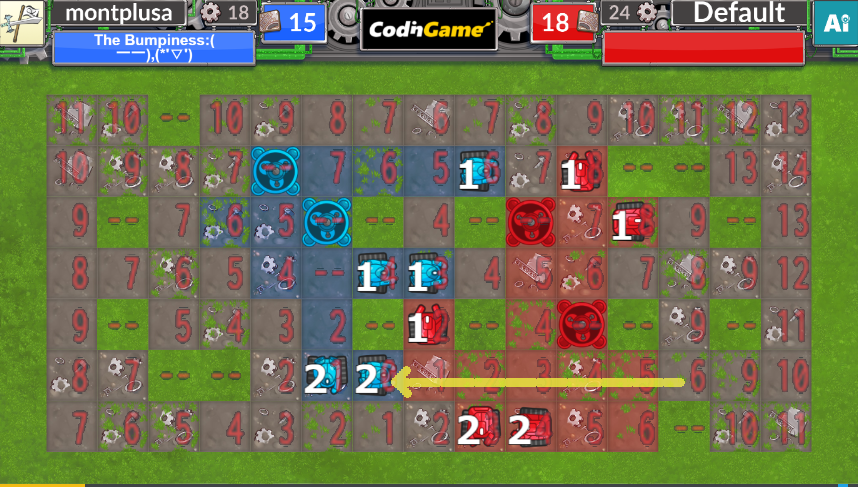
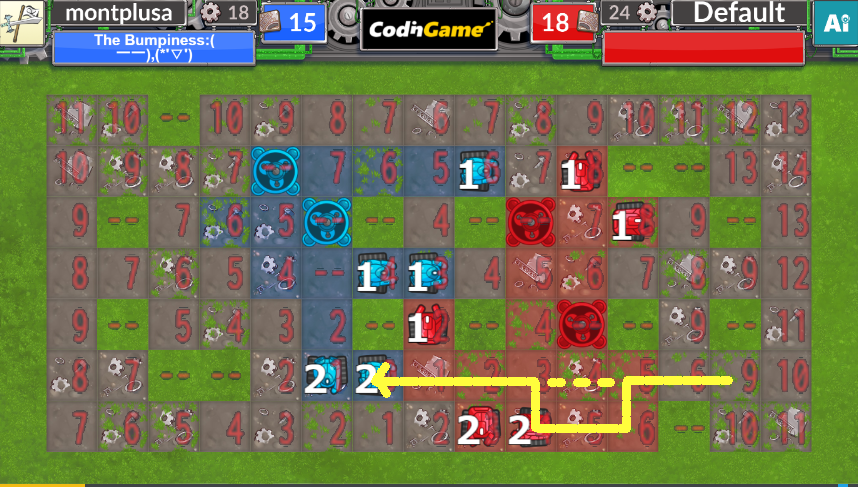
おおよそこれで行動を選択するのに必要な距離がすべて手に入りました。
(衝突地点の数が膨れ上がっていて3.が時間がかかってしまう可能性が指摘されそうですが、通常の試合ではその点は問題ありません。厳密には敵と市松模様のような模様をつくられると全地点間距離を求めることになり時間をオーバーしてしまいますが、こちらが協力して自陣に入れない限りはそうはならないです。)
解法の選択
これは良い手を探すのにどのような手法をとるかという他のコンテストを含めた話題になります。これはあくまでまだ新参者の自分の感覚で、一般的に正しいものであるというわけではないことにはご注意願いします。もしマラソン系、対戦系コンテストを始めて少しという方ならなんか得られるものがあるかも。逆にマラソン系、対戦系コンテスト玄人の方、ご指導ご鞭撻のほどよろしくお願いします。
問題のテーマによってどのような手法が適用しやすいかは変わってきます。ここでは、自分が適用したことのある手法と適用しやすいと感じる問題のタイプを書いておきます。解法自体の説明については自分が説明するよりも他サイトの素晴らしい解説を見たほうが良いので割愛します。
全探索
自分が全探索を使ったことがあるのはCodinGameのGreenCircleなど。
全探索の雰囲気は「いや、全部自前のシミュレーターで試したらいいやん」というもので、実際のところ、ゲーム終了までのすべてのパターンを試せるならこれが最強です。
ところが、大体のコンテストを見てみると、パターン数が膨大ですべてを試すことができないので、「1~3ターン先までの行動をすべて試す」or「ありえない手は外してもう少し先まで試す」という風に使っています。そもそも次ターン以降の自分の状況が予測不可能だったりする場合は消去法的によくこの手法を選んだりします。
全探索の場合、自分は評価関数はその盤面に将来性があるかなどを考慮して比較的複雑なものにする傾向があります。深さが浅い全探索自体には将来性が反映されていないのと、全探索は深さが1増えるとパターン数が跳ね上がるために多少高速化しても深さを1増やすことはできないからです。
例えば、CodinGameのGreenCircleでは、カードのドロー後からターン終了までの可能なアクションは相応に限られていたので1ターン全探索を行いました。逆にこのコンテストでは次ターン以降はカードのドロー次第で状況が変わるので読みづらいゲームでした。
ビームサーチ
自分がビームサーチを使ったことがあるのはCodinGameのMadPodRacing、SpringChallenge2021など。
ビームサーチと全探索はかなり近い手法と思っています。ビームサーチは評価値の上位のものだけ次のターンを考えていくことで全探索に比べて時間やコストを節約できます。
ターン制の対戦型コンテストにおいて、状況を得点化して、nターンの良さげな行動を探すというのが自分の中では多いです。しかし、ビームサーチ(と後述する焼きなまし)自体は相手の動きの影響に対して弱い(と私は思っている)ので、一ターンの敵の行動によって大きく状況が変わってしまうゲームよりは、敵の影響がある程度小さいゲーム、あるいは敵との衝突要素がないマラソン系だと考えやすいです。また、結構ターン(順序関係)を意識した手法な気がします。順序関係がないものでは無理やり順序関係を作ったり、重複を除去するなどの工夫が重要になりそうです。
ビームサーチの場合、自分は評価関数は盤面の将来性があるかなどを考慮しつつも全探索よりは軽めにする傾向があります。将来性をある程度見積もらないと数ターン後に盤面がよくなるような手がビームサーチの幅から外れてしまい探索できない可能性がある一方で、軽めにすることで幅が増やせたり、深さが深くなったりするのが理由です。
例えば、CodinGameのMadPodRacingは1ターンでマシンの向き変化はせいぜい18度ほどなので、1,2ターンでの敵の動きは台風の予測円みたいにある程度のぶれに収まります。したがって、敵の妨害などがある場合でも、敵がある程度巧みなプレイヤーでなければマシンを走行可能でした。
SpringChallenge2021は、1ターンに複数行動ができるゲームでしたが、1ターンに得られるマナ(いろんな行動のもとになるもの)がそれなりに少ないので行動数がある程度限られたことや、アクションが種を植える、木を育てる、収穫といった具合でユニットが移動するタイプではなかったので相手の影響はある程度小さいゲームでした。
山登り法・焼きなまし法
自分が山登り法を使ったことがあるのはCodinGameのSmashTheCodeなど。
また、ランダム+貪欲も個人的には山登りとほぼほぼ同じものだと思っています。
ビームサーチの場合だと「これをしてから、これをして・・・」というような順序関係が根本にあるのですが、山登りは順序関係がないものにも使いやすいです。今回のコンテストだと1ターンのユニットの動きは「どのユニットから動かす」みたいな要素がないので、ユニットを雑に動かして、山登りにより改善、みたいな発想もあるかもしれません。(私は当初はこの予定でした)
焼きなまし法は山登りの際に確率的に悪化するものを採用するということでかなり山登り法と近いものを感じます。採用しすぎると山登りよりも悪い結果になることもありますが、基本的には山登りよりもポテンシャルのある手法だと思います。(コンテスト期間中に実装した経験なし)
例えば、CodinGameのSmashTheCodeはいわゆる「ぷよ〇よ」だったのですが、相手による影響は「連鎖を打ってくるか打たないか」の二択だけだったので、打った場合と打たなかった場合で6手の置き方の山登りを行いました。「ぷよ〇よ」は手順のあるゲームですが、連鎖を組む行為がしばしば「一時的に連鎖をつぶす・連鎖を打たない」というタイプの行為になるので、途中段階での評価が難しく、ビームサーチを私はうまく使えませんでした。
モンテカルロ木探索(MCTS)
自分がモンテカルロ木探索を使ったことがあるのはCodinGameのUltimateTicTacToeなど。
モンテカルロ木探索は自分と相手が交互に手を打つ場合に使いやすいと感じています。特にボードに駒を交互に置いていくタイプのゲーム(〇×ゲーム、五目並べ、オセロなど)では手を適用するのが高速で、ランダムな手でゲームの最後までをシミュレーションするのもかなりすぐに終わるので回数を稼ぎやすく、使いやすいです。
一方で可能な手が多いタイプのゲームだと純粋に使うことはあまり効果が期待できなくて、ありえないと思われる手(五目並べで遠い彼方に駒を置くみたいな手など)を省くなどして対策するのがよさそうです。ゲームの最後までをランダムな手で実行するタイプの場合は評価値として勝ち/負けが利用できるので、良い手が人間では想像がつかない場合にも有効な気がします。
例えばCodinGameのUltimateTicTacToeは、いわゆる〇×ゲームの革命的な拡張版ですが、人間では何が良い手なのかいまいちわからない問題でした。一方でマスは9*9、出てくるマスは〇と×だけ、駒の移動もなしというゲームなので、ゲーム終了までランダムな手で実行するのは比較的高速でした。
MiniMax法
使ったことがあるのはCodinGameのUltimateTicTacToe(Goldリーグにいたころ)など。
この手法も交互着手だと使いやすいです。あらかじめ候補手を絞らない場合は全探索と同じ感覚だと認識しています。なお、αβ探索に切り替える(不要な計算を省く)ことで、思ったよりも先の手まで探索することができたりしました。
CodinGameのUltimateTicTacToeは交互に行動するタイプであったためにMiniMax法が利用できそうな問題でしたが、UltimateTicTacToeのゲーム性が難しく、うまい評価関数が見つからなかったためGoldで止まってしまいました。もちろんMiniMax法を使うLegendの人もいるので、Goldで止まるのは自分の力不足です。(ゲーム終了までシミュレートするMCTSに切り替えたところLegendに到達しました。)
今の自分はおおよそこんな理解です。まだコンテスト経験のない機械学習、遺伝的アルゴリズムなどはまだまだ感覚が得られていませんが、いつか挑戦できたらと思っている手法ではあります。
さて、今回の問題で考えてみると、大量の候補手やゲーム終了状態までの長さ、同時着手ということからMCTSは不向きだと思っていて、全探索やビームサーチもパターン数的にあり得ない手を削るor一つ一つのユニットを独立に扱う必要がありそうです。Minimax法も相手の動きを仮定してから自分の動きを決めてしまうのをある程度解消しなければという感じがしました。必然的に貪欲or山登りあたりが自分の手持ちかな・・・と考えてました。自分は機械学習は門外漢なので機械学習なんかも得意なタイプなんじゃないかなあなどと考えていましたが、マップのサイズやコード長制限など、機械学習にも困難があったみたいです。
この他if文の条件分岐のみで行動を決定したり、目標に向けて貪欲に行動を決定していくのも有効です。個人的には貪欲法を実装したら「多少のランダム性をつける&評価関数を作る」「部分的に破壊して適用し直す」へもっていくのが安心安全の流れだと思っています。
ところでルールベースっていったいどういう区分なんでしょう?自分の中では結構あいまいなんですが・・・。
おわりに
この駄文をここまで読んでくださった方いるんでしょうか・・・という感じですが、ここまで読んでいただきありがとうございます。今後のコンテストに向けて自分が成長できるように書いたものでもあるのですが、もし今読んでいる方のお役にも立てていたら幸いです。